Abstract
We calculate the engine efficiency of a Leidenfrost droplet transport system to assess application for various industrial processes. The engine relies on the Leidenfrost effect to transport water droplets in a straight line across a superheated aluminium surface with ratchet-like topography. The engine efficiency of such a system has not been calculated in the literature thus far. Acceleration-time data was collected using Logger Pro 3® motion-tracking software and mechanical work was calculated using a midpoint Riemann sum. A power meter measured total power input at a constant rate. Average trial times were used to determine the power input for each trial, and engine efficiencies were subsequently calculated. Droplet volume and ratchet angle were varied as parameters in attempt to optimize engine efficiency. Our results give an extremely low average percent efficiency (2.86E-07%), which agrees with previously reported results for an analogous turbine system, to an order of magnitude. Varying the ratchet angle does not affect engine efficiency to any statistically meaningful extent. Increasing droplet volume in the 15-35 µL range tends to marginally improve engine efficiency for steep ratchet angles.
Introduction
All compounds have characteristic phase-change temperatures. Past the boiling point of a compound, an interesting phenomenon can be observed which allows the compound to maintain liquid or even solid form while in contact with a superheated surface (Bernardin et al., 1999; Biance et al., 2003; Cole et al., 2015; Hashmi et al., 2012; Lagubeau et al., 2011; Linke et al., 2006; Ok et al., 2011; Quéré, 2013; Walker, 1994; Wells et al., 2015). Most famously, when a liquid water droplet is placed onto a superheated aluminium surface (hotter than its boiling temperature) a vapour layer instantaneously forms underneath the droplet, insulating the liquid water and thereby preventing its rapid evaporation. Water vapour conducts thermal energy approximately one order of magnitude lower than liquid water (Walker, 1994). The temperature at which the droplet exists for the longest time is called the Leidenfrost temperature. Near the Leidenfrost temperature, liquid water droplets can be maintained for several minutes (Biance et al., 2003; Lagubeau, et al., 2011; for review see Quéré, 2013).
As first demonstrated by Linke et al. (2006), liquid water droplets on a superheated metal slab with ratchet-like topography travel in a well-defined direction with a well-defined velocity. This locomotive force is thought to be caused by the exiting of vapour under the droplet directed by the asymmetric topography of the metal surface (Lagubeau et al., 2011, Linke et al., 2006). Following the successful proof-of-concept study (Linke et al., 2006), many practical applications have been envisioned for the Leidenfrost system. The low friction environment and lack of moving parts alludes to an efficient and potentially advantageous mechanism for transporting liquid, dissolved solutes, or supported objects. Hashmi et al. (2012) showed that multiple Leidenfrost drops traveling together could be harnessed to transport ‘carts’ weighing up to 50 g.
Cole et al. (2015) showed that it is possible to engineer the trajectory of a Leidenfrost droplet to be sensitive to surface temperature. This discovery opened up a wide possibility for feedback cooling mechanisms that do not rely on electrical or moving components. Ok et al. (2011) observed that ratchet-like structures can help injected droplets adhere to the hot metal surface. This allows for a controlled and continuous transfer of heat, a necessary requirement for fuel-injection and combustion systems, steam generators, cooling systems for nuclear reactors, and spray quenching systems (Ok et al., 2011).
The incentive to develop technologies that exploit the Leidenfrost effect motivates our present work. The engine efficiency of a system that relies on the Leidenfrost effect to produce mechanical work in a straight line has not been previously calculated in the literature. However, Wells et al. (2015) constructed a Leidenfrost turbine which applies a torque to a solid carbon-dioxide disk, producing rotational motion. Their system relied on a similar ratchet like-topography to turn a dry-ice disk which sublimated on contact with a superheated aluminium surface (Wells et al., 2015). The engine efficiency of the turbine system was reported to be on the order of 1E-06%. In our experiment, two parameters thought to affect the dynamics of the water droplet were examined: ratchet angle and droplet volume. These parameters were varied within reasonable values based on the available literature.
Methods
Aluminium slabs were machined to have an asymmetric ratchet-like surface topography (Fig. 1). Table 1 provides the dimensions of the machined aluminium slabs with 15° and 30° ratchet angles. These dimensions closely resemble those studied by Linke et al (2006). The slabs were positioned on a hot-plate perpendicular to a Canon T3i® DSLR camera and a thermocouple was used to monitor the surface temperature of the slabs. One end of the thermocouple was placed in a beaker of ice-water (0° Celsius) and the other was coiled tightly around an accessory aluminium slab, used as a weight, to measure hotplate surface temperature. The camera was mounted level to the experimental setup to record position-time data. A magnetic-assist pipette was used to control the droplet volume which was varied between 15-35 µL in 5 µL increments. Droplets of this size reliably accelerated in the expected direction, did not spontaneously divide, and could be manually deposited onto the superheated surface with relative ease. A water droplet accelerating due to the Leidenfrost effect after pipetting is shown in Fig. 2.


The hotplate was heated to a temperature well above boiling (335° Celsius), slightly hotter than the recorded Leidenfrost temperature for water on aluminium (Bernardin et al., 1999). The aluminium surface temperature remained relatively constant throughout (± 7°C) and was monitored closely during experimentation using a thermocouple. The entire experimental setup is shown in Fig. 3.

Initial tests suffered from an unreliable and inconsistent way of depositing stationary droplets on the heated aluminium surface. An established protocol (Table 2) was implemented and determined which replicates would contribute to the average engine efficiency. The protocol ensured the water droplets were initially stationary and were only accelerating due to the Leidenfrost effect. Recorded videos of the accepted replicates were analysed using Logger Pro 3® motion-tracking software. The known length of the ramp was used as a calibration scale.
Efficiency calculation
Energy efficiency was calculated by measuring the mechanical work done on the Leidenfrost droplet and the energy input from the hotplate, as summarized by the following equation:
\textit{Efficiency}=\left(\frac{\textit{Work}}{\textit{Energy input}}\right)\times100Work refers to mechanical work done in the direction perpendicular to the aluminium ratchets, across the full length of the slab. The work for a given replicate was calculated by numerically integrating the force function with respect to position, similar to the method used by Linke et al. (&2006).
\textit{Work}=\int^{x}\vec{F}\left(x'\right)\cdot dx'Position, velocity, and acceleration was determined using Logger Pro 3® software and a Canon T3i shooting at 60fps. Acceleration in the direction across the full length of the aluminium slab was considered work; all other acceleration was considered a system inefficiency. Using Newton’s second law and the known mass of the water droplet, force was calculated as a function of position. The mass for each water droplet was calculated using the known droplet volume and the density of water at room temperature (1g/mL). The droplet density was assumed to be that at room temperature as the droplet was well-insulated by the vapour layer.
Instantaneous acceleration was calculated by taking the second-order time derivative of the position-time data using finite difference in Logger Pro 3®. The change in position between each time step was calculated using position-time data, converting acceleration as a function of time to acceleration as a function of position (relative to the initial starting position of the droplet). After obtaining force as a function of position, a midpoint rule Riemann sum with a 16.683 ms time-step was used to numerically approximate Eq. (2). The standard deviation for work was calculated between replicates of the same trial (same droplet volume and ratchet angle).
Energy input was measured using a power meter. The power input was monitored over a three-hour period and a constant power input of 266.67 J/s was observed. The energy input for a given replicate was calculated by multiplying the total time the water droplet spent in contact with the aluminium slab, by the constant power input. Uncertainty in the power measurement was defined as the digital uncertainty in the power meter:
\textit{Energy input}=\textit{Replicate time}\times266.67\textup{J/s}Results
To determine if we had reproduced the experimental conditions of Linke et al. (2006), we measured the average acceleration as a function of droplet volume. Comparing with their Fig. 5, our average droplet acceleration for 15° ratchet angle and 30 µL droplet volume, was 0.245 m/s2, which agrees with the value obtained by Linke et al. for 30 µL to one significant figure.
Figures 4 & 5 show the engine efficiency versus droplet volume for Slabs 1 & 2 respectively (see Table 1). Fig. 4 shows a relatively large standard deviation for the 30 µL trial which motivated us to double the sample size. After taking more measurements, the relatively large standard deviation persisted. The sample size was similarly doubled for 30 µL in Fig. 5 to allow for a comparison between ratchet angles. A least-squares fit was performed to determine the linearity of the relationship. For the steeper 30° ratchet angle, increasing droplet volume in the 15-35 µL range tends to marginally improve engine efficiency. The low R2 value in Fig. 5 does not support a similar trend for the shallower 15° ratchet angle.
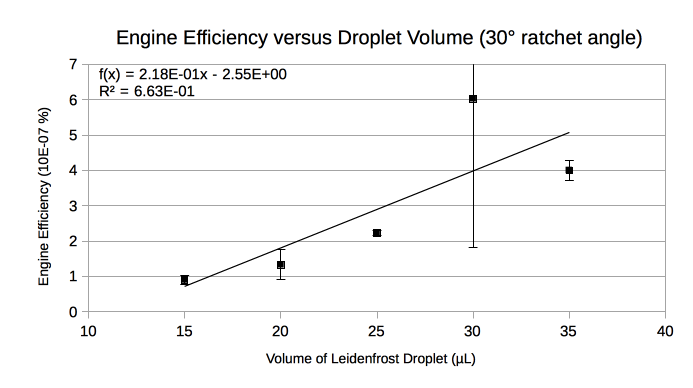
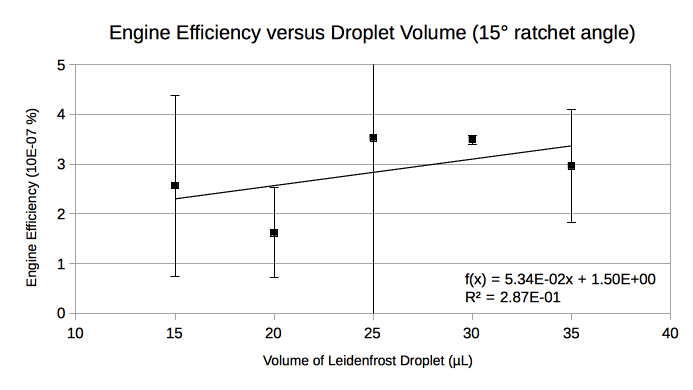
Our Leidenfrost droplet transport system had an extremely low average percent efficiency: 2.86E-07%. This is because the average work done on a Leidenfrost droplet was extremely low relative to the energy input. The extremely low engine efficiency is not dissimilar to that obtained by Wells et al. (2015) which was reported to be on the order of 1E-06%.
Table 3 compares the mean engine efficiencies between the aluminium slabs with 30° and 15° ratchet angles. A two-sample t-Test for equal means was used to infer a change in mean efficiency between slabs:
T=\frac{\mu_1-\mu_2 }{\sqrt{\frac{\left(\sigma_1\right )^2}{N_1}+\frac{\left(\sigma_2\right )^2}{N_2}}} μ1 and μ2 are the sample means for Slab 1 and Slab 2 respectively, σ1 and σ2 are the sample standard deviations, and N1 and N2 are the sample sizes. A p-value (two-tailed), was generated from the two sample T-test. A p-value greater than 0.05 does not allow one to conclude that varying ratchet angle from 30° to 15° has a statistically meaningful effect on engine efficiency.
μ1 and μ2 are the sample means for Slab 1 and Slab 2 respectively, σ1 and σ2 are the sample standard deviations, and N1 and N2 are the sample sizes. A p-value (two-tailed), was generated from the two sample T-test. A p-value greater than 0.05 does not allow one to conclude that varying ratchet angle from 30° to 15° has a statistically meaningful effect on engine efficiency.
Discussion
The discrepancy between our calculated engine efficiency and the engine efficiency calculated by Wells et al. (2015) may be explained by the difference in exposed hotplate area. Hotplate area that is not in direct contact with the aluminium slab heats the surrounding air which does not contribute to the total work. The exposed hotplate area in our experimental setup seems to be larger than the exposed hotplate area in Wells et al.’s (2015) experiment. The discrepancy may also be explained by the difference in transport load. The maximum load for an insulated carbon-dioxide disk is much larger than the maximum load for a stable water droplet. A larger load would increase the work done and therefore increase engine efficiency.
In order to reach the Leidenfrost temperature of water, a large amount of input energy was required. Liquids with lower Leidenfrost temperatures would decrease the required energy input and therefore increase engine efficiency. Moreover, Leidenfrost ‘carts’ could increase engine efficiency. In a recent development by Hashmi et al., loads as massive as 50 g were supported by multiple Leidenfrost droplets travelling together. A higher load capacity could dramatically increase the engine efficiency of a Leidenfrost droplet transport system and a similar calculation to our present work should be performed for the ‘cart’ system.
Varying the droplet volume and ratchet angle within the experimental values did not have a major effect on engine efficiency. Efficiency optimization must be achieved by varying other parameters such as ratchet size (Ok et al., 2011), or by making significant design changes to the system.
Conclusion
The engine efficiency of a Leidenfrost droplet transport system, which transports droplets in a straight line, was calculated. Our results give an extremely low average percent efficiency (2.86E-07%), which agrees with the result from Wells et al. (2015) for an analogous turbine system, to an order of magnitude. Differences in exposed hotplate area and maximum load between the two experiments may explain the difference in calculated engine efficiency. Droplet volume and ratchet angle were varied in an attempt to optimize engine efficiency. Varying the ratchet angle does not affect efficiency to any statistically meaningful extent. Increasing droplet volume in the 15-35 µL range tends to marginally improve engine efficiency for steep ratchet angles. Further optimization must therefore be achieved by varying other parameters such at ratchet size or by making significant design changes to the system. Leidenfrost ‘carts’, which rely on multiple Leidenfrost droplets travelling together to support more massive loads, may provide a mechanism to dramatically increase the engine efficiency of a Leidenfrost droplet transport system.
Acknowledgements
The authors would like to thank Dr. James Charbonneau for his mentorship, as well as the Science One programme for incentivizing early undergraduate research.
References
- Bernardin, J. D., & Mudawar, I. (1999). The Leidenfrost Point: Experimental Study and Assessment of Existing Models, Journal of Heat Transfer 121, 894-903.
- Biance, A., Clanet, C., & Quéré, D. (2003). Leidenfrost drops, Physics of Fluids 15, 1632-1637.
- Cole, A., Jury, B., & Takashina, K. (2015). A Leidenfrost Thermostat, Journal of Heat Transfer 137, 034502.
- Hashmi, A., Xu, Y., Coder, B., Osborne, P. A., Spafford, J., Michael, G. E., Yu, G., & Xu, J. (2012). Leidenfrost levitation: beyond droplets, Scientific Reports 2, 797-801.
- Lagubeau, G., Le Merrer, M., Clanet, C., & Quéré, D. (2011). Leidenfrost on a ratchet, Nature Physics 7, 395-398.
- Linke, H., Alemán, B. J., Melling, L. D., Taormina, M. J., Francis, M. J., Dow-Hygelund, C. C., Narayanan, V., Taylor, R. P., & Stout, A. (2006). Self-Propelled Leidenfrost Droplets, Physical Review Letters 96, 154502.
- Ok, J. T., Lopez-Oña, E., Nikitopolus, D. E., Wong, Harris., & Park, S. (2011). Propulsion of droplets on micro- and sub-micron ratchet surfaces in the Leidenfrost temperature range, Microfluidics and Nanofluidics 10, 1045-1054.
- Quéré, D. (2013). Leidenfrost dynamics, Annual Review of Fluid Mechanics 45, 197-215.
- Walker, J. (1994) Boiling and the Leidenfrost effect, Physics Education 29, 39-42.
- Wells, G. G., Ledesma-Aguilar, G. G., McHale, G., Sefiane, K. (2015). A sublimation heat engine, Nature Communications 6, 6390.
